
 Share This Page
Share This Page| Home | | Mathematics | | * Applied Mathematics | |  |  Share This Page Share This Page |
Please read this Disclaimer
![]() Anaglyphic:
Transparency:
Anaglyphic:
Transparency:
Figure 1: A storage tank with a sloped bottom section
Since I origially wrote TankCalc years ago, I've gotten requests to write equations and compute values for any number of strange tank shapes. Every once in a while I get a request that's reasonable and practical enough to pursue an analysis. The tank described here falls into that category, and I hope it's common enough for this analysis to be useful.
Here's an excerpt from the original request:
I have an interesting problem here at work. We have a series of fermentors that are vertical cylinders but have a sloped base. Once the level is above the cylindrical wedge section, volume calculations are trivial. The issue is in trying to model volume of any given horizontal section of the cylindrical wedge.
I can find methods for calculating the volume using vertical sections of the wedge - but liquid is not quite nice enough to stand on end in infinitesimal slices so these do not work.
Have you any methods by which I could calculate the volume?Some requests have an infelicitous combination of rarity and mathematical difficulty, but this one isn't too difficult, and it's my hope that there are more such tanks out there so this analysis will prove useful to others.
When confronted by a tank like this, with different properties in different areas, I adopt a zone approach — one solution for zone A, another solution for zone B, ad infinitum. This means the solution for the entire tank is more algorithmic than algebraic, but this is, after all, applied mathematics, and most people who inquire want practical, numerical results.
Before we start, please notice about Figure 1 above that it's not just a graphic image, it's a three-dimensional model that readers can manipulate with their pointing devices. Drag your mouse cursor across the display to rotate the modeled tank, and use your mouse wheel to zoom in and out. And if you happen to have a set of
red-blue glasses, by all means activate the anaglyphic mode and see the model in real 3D.
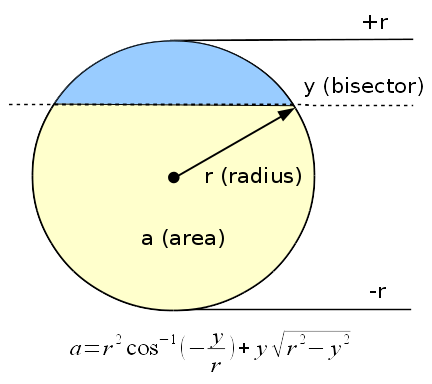
Figure 2: Equation for partial circle areas (from TankCalc)
Analysis of partial volumes of this tank type can be broken down into two subproblems:
To analyze the sloped section, I decided to use a method I created for TankCalc — see Figure 2. The equation is:
- The easy part — the cylindrical section above the slope, which has a volume of:
(1) $ \displaystyle v = \pi r^2 h$
- v = volume
- r = tank radius
- h = cylindrical section height
- More difficult — the tank's sloped section, which lies between the tank's bottom and the top of the slope where the tank becomes a cylinder. There's no simple, closed-form equation for this part.
(2) $ \displaystyle a = r^2 \cos^{-1} \left(-\frac{y}{r} \right) + y \sqrt{r^2-y^2} $
- a = partial circle area at position y:
$ 0 \leq a \leq \pi r^2$- y = bisector position in circle:
$ -r \leq y \leq r$- r = tank radius
But unlike its original application, in this case the computed partial circles lie horizontally, on the plane of the tank's liquid contents, and follow the profile of the tank's sloped section. In this method, we model the sloped section as a series of horizontal two-dimensional slices, then sum them to create a volume result. More formally, we generate this sum:
(3) $ \displaystyle f(y) = r^2 \cos^{-1} \left(-\frac{y}{r} \right) + y \sqrt{r^2-y^2} $ (circle partial area, equation (2))
(4) $ \displaystyle g(h) = f(\frac{(h-a) 2r }{ b-a}-r) $ (interpolate sensor height h in {a, b} to circle area y in {-r,r})
(5) $ \displaystyle v = \frac{b-a}{n+1} \sum_{x=0}^n g((b-a)\frac{x}{n}+a) $ (sum circle areas for volume result)
Now let's create some results.
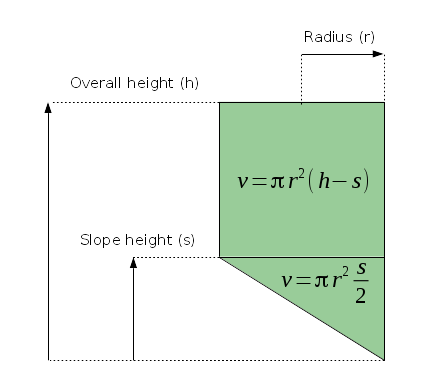
Figure 3: layout and full-volume equations
This section contains a volume computer based on the above analysis. It generates volume values based on user entries for the class of tank shown in Figure 1. Remember that you may use any convenient units, as long as you're consistent. The computer only requires three entries (use Figure 3 for guidance):
- The tank's radius (r):
- The tank's overall height (h):
- The height of the sloped section (s):
Here are the results for the entered quantities:
- Tank cylindrical section volume:
- Tank sloped section volume:
- Tank total volume:
This section generates a table correlating sensor heights to partial volumes. Be sure you've entered the tank's dimensions in the "Volume Computer" section above. Each table row contains a sensor height and a corresponding partial volume. The table generator uses these additional values:
- Sensor height step size:
- Integration steps:
To create a table based on current entries, press or
To copy the table to your system clipboard:
- Click inside the table display.
- Press Ctrl+A or choose menu item "Select All".
- Press Ctrl+C or choose menu item "Copy".
For database and spreadsheet purposes, choose the CSV table option — it's much easier to import to other applications.
First, before creating this page I wrote a Python program to generate and check the method for errors. For those who don't want to be tied to a Web browser, this Python listing produces the same results this page does.
Second, there are some ways to be sure you're getting accurate results from this method. When generating tables, it's always a good idea to verify certain results that are available in closed form. These equations should serve as a basis for result testing:
(6) $ \displaystyle v = \pi r^2 (h-s) $ (cylindrical section volume)
(7) $ \displaystyle v = \pi r^2 \frac{s}{2} $ (sloped section volume)
(8) $ \displaystyle v = \pi r^2 (h - \frac{s}{2}) $ (total tank volume)
When the sensor height equals the height of the sloped tank section, the listed volume should equal the result for equation (7). The last row in the table, representing 100% volume, should equal the result for equation (8).
I apologize for the strict legalese below, but the calculations described here may be used to design and maintain fuel tanks and the possibilities for litigation have not escaped my attention. Sorry. Disclaimer of WarrantyThe computations and methods described here are provided on an "as-is" basis, without warranty of any kind, including without limitation the warranties of merchantability, fitness for a particular purpose and non-infringement. The entire risk as to the quality and performance of the computations is borne by you. Should the results prove to be in error, you assume the entire cost of any required service and repair, and any consequential damage.Limitation of LiabilityAs customary in the computer business, you are solely responsible for any loss of profit or any other commercial damage, including but not limited to special, incidental, consequential or other damages. This disclaimer specifically disclaims all other warranties, expressed or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose, related to defects in the computed results or the documentation.
| Home | | Mathematics | | * Applied Mathematics | |  |  Share This Page Share This Page |