Here's how I would proceed — for the sloped part, write an equation for the area of the sloped section as a triangle with the same angles (just use the height argument as the height of the triangle), then to get a volume for the computed area, simply multiply by the length of the sloped area.
Then, for the rectangular part, it's simply width times length times that section's height minus the sloped part. Then add that computed volume to the volume you already computed for the sloped part.
One more thing — a container with a two-way slope can be computed as though it has only one slope. Just figure out the width of the container at each vertical height. Once you've done that, it no longer matters how you picture it, because the widths at each height are the same whether there are one or two slopes. To see this, cut up some cards with different widths and stack them. You will see that it doesn't matter whether they're centered or the cards are lined up on one side, the volume is the same.
As it happens, after writing yesterday, I worked on this problem some more. My solution assumes a rectangular tank with a double-slope bottom section, sort of like the inside of a boat, but with an important difference — the Z axis must have the same size at all heights. Here's my solution:
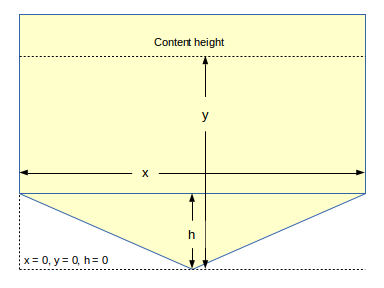
Figure 1
The tank has three dimensions — x, left-right on the page, y, up-down on the page, and z (not shown above), in and out from the plane of the page. The sloped shape at the bottom is limited to the x and y dimensions, the z dimension has the same size at all heights. And the y dimension's zero point is located at the bottom of the tank (bottom dashed line as shown above).
Incremental volumes for this tank are acquired in two separate solutions that depend on whether the y content height is greater than or equal to the "h" height value.
If the y content height is less than "h", the solution volume "v" is equal to:
\begin{equation}
v = \frac{x y^2 z}{2h}
\end{equation}
If the y content height is greater than or equal to "h", the solution volume has two parts:
Part one (the part of the tank above "h"):
\begin{equation}
v = x (y-h) z
\end{equation}
Part two (the part below "h", which is now constant):
\begin{equation}
v = \frac{x h z}{2}
\end{equation}
Simply add Part 1 to Part 2.
On that basis, the complete volume equation for y >= "h" is:
\begin{equation}
v = [(y-h) x + \frac{x h}{2}] z
\end{equation}
A typical embodiment for this solution would be a computer program that would first determine whether y is greater than or equal to "h", then select the correct method on that basis.
Here's an example Python program that solves for this tank shape — remember for this method to work, the Z dimension must have a fixed size:
Here is a plain-text listing for the above program.


 Share This Page
Share This Page

 Share This Page
Share This Page

 Share This Page
Share This Page