This will take some telling. Electric Duet is a classic Apple ][ program that did a lot with a little. In truth, any Apple ][ program that did something noteworthy constituted doing a lot with a little, because by modern standards, the Apple ][ was an extraordinarily weak machine — there are now pencil sharpeners that have more raw processing power than the original Apple ][. Notwithstanding that fact, in the context of its time, the Apple ][ was an extraordinary breakthrough.

Figure 1: Apple ][ speaker schematic

To tell this story, I ask that my readers, more than half of whom probably weren't born when I wrote Electric Duet, imagine a time when there was no Internet, in fact no personal computer networks at all, when sixteen kilobytes was regarded as a lot of memory, and when a respectable mass storage device could hold 140 kilobytes. When a clock speed of one megahertz was regarded as respectable (a typical modern computer clock speed, 2 gigahertz, is 2,000 times faster).

Figure 2: My Oregon cabin

Now imagine an electronic consumer product whose designers want to make a simple "beep" sound under certain conditions, but without costing too much or unduly adding to complexity. If I were designing it, I would attach a cheap speaker to the output of a TTL device (Figure 1) — a simple binary gate that is either on or off — either true or false, either 1 or 0. Then I would clock the gate at some suitable frequency for a quarter-second — beep. Done.

Next, imagine there's a guy living in a hand-built cabin in the Oregon woods (Figure 2), with lots of leisure time on his hands, and who thinks a personal computer is the most wonderful thing imaginable. He has a new Apple ][, and he can't think of anything more fun than seeing how much performance he can squeeze out of it.

Remember, dear reader, this was an innocent time, a time not at all like the present — a time when computers were instruments for creativity, not larceny.

Figure 3: Square-wave tone generator

After familiarizing myself with the Apple ][, I wrote a simple program that played a crude kind of music — just square waves of fixed duration.

Modern programmers might want a word of explanation — in 1977, when I wrote the code shown in Figure 3, the Apple ][ had a primitive BASIC interpreter that couldn't do very much and couldn't manipulate the machine's hardware. Programmers quickly discovered that to get interesting results, one needed to write 6502 assembly-language code. As it happens, because of the lack of usable high-level languages, every Apple ][ program I wrote then or later, was written in assembly language — Apple Writer, Apple World, the subject of this article, and many others.

The simple generator shown in Figure 3 created some excitement at Apple and was included in the 1978 Apple ][ Reference Manual (page 45) — with my name misspelled. But there was more to come.

Figure 4: Musicomp screen shot

My next project was a more elaborate music editor-generator called Musicomp (Figure 4), which Apple bought and marketed. Here's a sample of how it sounded.

Even though its output was rather crude, compared to the simple square waves that preceded it Musicomp represented a big step forward because I began to control the speaker waveform's "duty cycle", i.e. the percentage of time the speaker was activated during each cycle of the tone. This change had the effect of making the sound almost acceptable, perhaps only to someone both young and in love with comparatively primitive technology.

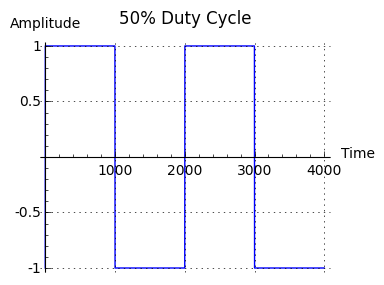
The idea behind controlling a square wave's duty cycle is that by doing so, one controls both volume and spectrum. A Fourier analysis of square waves having different duty cycles produces this result:

Time Domain		Frequency Domain
	->
	->

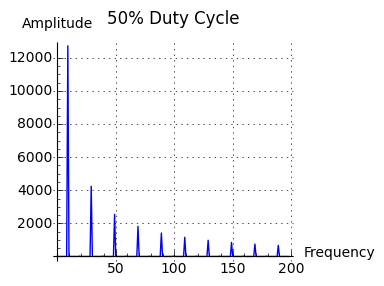
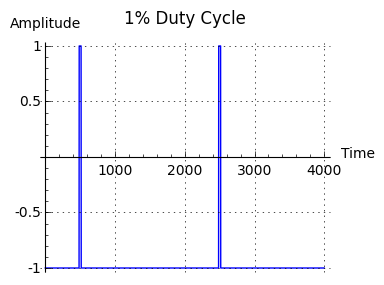
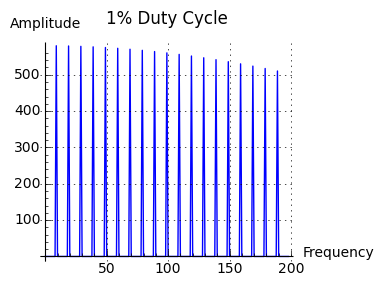Figure 5: Effect of duty cycle on frequency spectrum

Notice about Figure 5 that decreasing the duty cycle of the generating waveform increases the amplitude of high-frequency components while reducing the overall volume. This theoretical effect is easily audible — click here to observe how a progressive change in duty cycle changes the spectrum of a sound whose frequency remains constant.

Considering the simple circuit it used for output, and in spite of its crude sound, Musicomp blew some minds, but this bore no comparison to what happened next.

After finishing Musicomp, for a while I was distracted writing Apple Writer, a very successful project. In my spare moments I continued to think about the possibilities for further improvement in Apple ][ sounds. I wondered whether it might be possible to play two notes simultaneously, each with independent duty cycle control. That would represent a real musical resource, something beyond the toylike sounds of Musicomp.

Figure 5: Electric Duet Time-domain
Multiplexing Scheme

After some reflection I was able to imagine a theoretical scheme to accomplish this, but it wasn't obvious how to implement it in code. The basic idea behind Electric Duet is to switch between two independently generated square waves at a very high rate — the higher the better, ideally above human hearing — and rely on a combination of speaker response and human hearing limitations to create the illusion that two notes are being played simultaneously.

Figure 5 only hints at how this idea was expected to work. In practice, the program would switch between the red and green waveforms at a rate much higher than the frequencies of the notes being played, as well as change the duty cycles (dotted lines) as required by the music.

Before starting to code, I summarized the algorithm's requirements:

1. The algorithm would have to cycle the speaker's driving voltage at a precise rate, with no variation regardless of what the program was doing, for two voices, each having a number of possible duty cycles, while the program was also reading an array of notes and rests and monitoring the computer's keyboard so the user could interrupt the performance.
2. Item (1) above meant that the control loop would have to use the same number of machine cycles regardless of what it was doing. If it branched from one location to another, it would have to do so without changing the total number of machine cycles in the control loop. If this requirement were not met, the music would change duration or pitch while playing.
3. While reading the data array and driving the speaker, the algorithm would have to assign each note and rest a consistent time value, with no variation. I added this requirement because of a defect in Musicomp — after each note, Musicomp would redraw the music display, which created pauses in the music that were not accounted for in the musical score. Depending on the duration of the notes, this defect produced tempo changes that a perfectionist would find unacceptable.

Because by that time I had written a number of large assembly-language programs, I had no illusions about how difficult this program would be to create. Assembly language programming is difficult enough without worrying about the number of machine cycles each instruction requires.

As the project got underway I experimented with various schemes for simultaneously reading an array of note frequencies, durations and duty cycles, while driving the speaker with two independent frequencies and also monitoring the system keyboard. Because of the Apple ][ clock speed (1.023 MHz) and the number of machine cycles required by typical instructions, I realized that the switching frequency wouldn't be nearly as high as I would have liked — it ended up being about 8 KHz, easily heard by someone younger than about 50. Also, because the frequencies were defined in single bytes, the accuracy of the frequencies was limited, particularly for the higher notes.

After several weeks of work on the player code block, certainly the longest time spent on a small bit of code in a long career, I had gotten the loop to play nearly accurate pitches with nearly constant loop timing. Finally, in a sort of chess match against a very patient opponent, I added one final no-operation placeholder instruction to correct a timing error, and discovered that change forced the control loop to always have the exact same duration regardless of the path through the loop, and coincidentally caused middle A (440 Hz) to fall within one hertz of the correct value. I realized I was done.

Here is a listing of the Electric Duet player routine, in 6502 assembly-language instructions, with the number of required machine cycles for each instruction alongside:

/***************************************************************************
 *   Copyright (C) 1979-2015 by Paul Lutus                                 *
 *   http://arachnoid.com/administration                                   *
 *                                                                         *
 *   This program is free software; you can redistribute it and/or modify  *
 *   it under the terms of the GNU General Public License as published by  *
 *   the Free Software Foundation; either version 2 of the License, or     *
 *   (at your option) any later version.                                   *
 *                                                                         *
 *   This program is distributed in the hope that it will be useful,       *
 *   but WITHOUT ANY WARRANTY; without even the implied warranty of        *
 *   MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the         *
 *   GNU General Public License for more details.                          *
 *                                                                         *
 *   You should have received a copy of the GNU General Public License     *
 *   along with this program; if not, write to the                         *
 *   Free Software Foundation, Inc.,                                       *
 *   59 Temple Place - Suite 330, Boston, MA  02111-1307, USA.             *
 ***************************************************************************/

/* Electric Duet Player Routine circa 1980 */
 
$0900> A9 01:   LDA #$01        ; 2 *!*
$0902> 85 09:   STA $09         ; 3
$0904> 85 1D:   STA $1D         ; 3
$0906> 48:      PHA             ; 3
$0907> 48:      PHA             ; 3
$0908> 48:      PHA             ; 3
$0909> D0 15:   BNE $0920       ; 4 *!*
$090B> C8:      INY             ; 2
$090C> B1 1E:   LDA ($1E),Y     ; 5 *!*
$090E> 85 09:   STA $09         ; 3
$0910> C8:      INY             ; 2
$0911> B1 1E:   LDA ($1E),Y     ; 5 *!*
$0913> 85 1D:   STA $1D         ; 3
$0915> A5 1E:   LDA $1E         ; 3 *!*
$0917> 18:      CLC             ; 2
$0918> 69 03:   ADC #$03        ; 2 *!*
$091A> 85 1E:   STA $1E         ; 3
$091C> 90 02:   BCC $0920       ; 4 *!*
$091E> E6 1F:   INC $1F         ; 5
$0920> A0 00:   LDY #$00        ; 2 *!*
$0922> B1 1E:   LDA ($1E),Y     ; 5 *!*
$0924> C9 01:   CMP #$01        ; 2
$0926> F0 E3:   BEQ $090B       ; 4 *!*
$0928> B0 0D:   BCS $0937       ; 4 *!*
$092A> 68:      PLA             ; 4
$092B> 68:      PLA             ; 4
$092C> 68:      PLA             ; 4
$092D> A2 49:   LDX #$49        ; 2 *!*
$092F> C8:      INY             ; 2
$0930> B1 1E:   LDA ($1E),Y     ; 5 *!*
$0932> D0 02:   BNE $0936       ; 4 *!*
$0934> A2 C9:   LDX #$c9        ; 2 *!*
$0936> 60:      RTS             ; 6
$0937> 85 08:   STA $08         ; 3
$0939> 20 2D09: JSR $092D       ; 6
$093C> 8E 8309: STX $0983       ; 4
$093F> 85 06:   STA $06         ; 3
$0941> A6 09:   LDX $09         ; 3 *!*
$0943> 4A:      LSR A           ; 2
$0944> CA:      DEX             ; 2
$0945> D0 FC:   BNE $0943       ; 4 *!*
$0947> 8D 7C09: STA $097C       ; 4
$094A> 20 2D09: JSR $092D       ; 6
$094D> 8E BB09: STX $09BB       ; 4
$0950> 85 07:   STA $07         ; 3
$0952> A6 1D:   LDX $1D         ; 3 *!*
$0954> 4A:      LSR A           ; 2
$0955> CA:      DEX             ; 2
$0956> D0 FC:   BNE $0954       ; 4 *!*
$0958> 8D B409: STA $09B4       ; 4
$095B> 68:      PLA             ; 4
$095C> A8:      TAY             ; 2
$095D> 68:      PLA             ; 4
$095E> AA:      TAX             ; 2
$095F> 68:      PLA             ; 4
$0960> D0 03:   BNE $0965       ; 4 *!*
$0962> 2C 30C0: BIT $C030       ; 4
$0965> C9 00:   CMP #$00        ; 2
$0967> 30 03:   BMI $096C       ; 4 *!*
$0969> EA:      NOP             ; 2
$096A> 10 03:   BPL $096F       ; 4 *!*
$096C> 2C 30C0: BIT $C030       ; 4
$096F> 85 4E:   STA $4E         ; 3
$0971> 2C 00C0: BIT $C000       ; 4
$0974> 30 C0:   BMI $0936       ; 4 *!*
$0976> 88:      DEY             ; 2
$0977> D0 02:   BNE $097B       ; 4 *!*
$0979> F0 06:   BEQ $0981       ; 4 *!*
$097B> C0 00:   CPY #$00        ; 2
$097D> F0 04:   BEQ $0983       ; 4 *!*
$097F> D0 04:   BNE $0985       ; 4 *!*
$0981> A4 06:   LDY $06         ; 3 *!*
$0983> 49 40:   EOR #$40        ; 2 *!*
$0985> 24 4E:   BIT $4E         ; 3
$0987> 50 07:   BVC $0990       ; 4 *!*
$0989> 70 00:   BVS $098B       ; 4 *!*
$098B> 10 09:   BPL $0996       ; 4 *!*
$098D> EA:      NOP             ; 2
$098E> 30 09:   BMI $0999       ; 4 *!*
$0990> EA:      NOP             ; 2
$0991> 30 03:   BMI $0996       ; 4 *!*
$0993> EA:      NOP             ; 2
$0994> 10 03:   BPL $0999       ; 4 *!*
$0996> CD 30C0: CMP $C030       ; 4
$0999> C6 4F:   DEC $4F         ; 5
$099B> D0 11:   BNE $09AE       ; 4 *!*
$099D> C6 08:   DEC $08         ; 5
$099F> D0 0D:   BNE $09AE       ; 4 *!*
$09A1> 50 03:   BVC $09A6       ; 4 *!*
$09A3> 2C 30C0: BIT $C030       ; 4
$09A6> 48:      PHA             ; 3
$09A7> 8A:      TXA             ; 2
$09A8> 48:      PHA             ; 3
$09A9> 98:      TYA             ; 2
$09AA> 48:      PHA             ; 3
$09AB> 4C 1509: JMP $0915       ; 3
$09AE> CA:      DEX             ; 2
$09AF> D0 02:   BNE $09B3       ; 4 *!*
$09B1> F0 06:   BEQ $09B9       ; 4 *!*
$09B3> E0 00:   CPX #$00        ; 2
$09B5> F0 04:   BEQ $09BB       ; 4 *!*
$09B7> D0 04:   BNE $09BD       ; 4 *!*
$09B9> A6 07:   LDX $07         ; 3 *!*
$09BB> 49 80:   EOR #$80        ; 2 *!*
$09BD> 70 A3:   BVS $0962       ; 4 *!*
$09BF> EA:      NOP             ; 2
$09C0> 50 A3:   BVC $0965       ; 4 *!*
              

I have a special reason for including this listing — obviously it won't be of interest to many readers, but I have recently been trying to release this classic player algorithm under the GPL, and the GPL requires that a source listing be made available. The above listing is the official source for the Electric Duet player module.

To a modern programmer, calling the above listing "source code" may seem like an exaggeration, but this is only because modern programming is much more abstract than it was at the time I wrote Electric Duet. At that time there were no math coprocessors, no floating-point packages or libraries (at least for the Apple ][), and no compilers to translate powerful, abstract instructions into many more low-level machine code instructions. The above listing is machine code, and it's also the Electric Duet player source.

I had originally intended to include comments alongside each instruction in the above listing, but I quickly realized the comments would in some cases run to several lines to properly explain what is happening.

The above scheme only worked because the early Apple ][ machines had no interrupts, so the processor clock rate was reliable and accurately reflected wall time. Once the first interrupt was added to the Apple product line (to support a mouse), my program stopped working as intended.

Here are some samples of how Electric Duet sounds — actually, because of modern sound hardware and processing and because of the elimination of the time-domain switching frequency, much better than it sounded on an Apple ][:

• Bourree 1
• Bourree 2
• Fughetta 1
• Fur Elise
• Invention 1
• Invention 10
• Menuet 1
• Prelude
• The Entertainer

I wrote my first Apple music program in 1977, a mere 38 years ago. Because of the velocity of technological change, my early programs are historical artifacts, curiosities, indeed that was true ten years after they were written. In my time I've watched transistors replace vacuum tubes, integrated circuits replace transistors, and computers replace adding machines and slide rules (both of which I've used at some point in my career). When I designed circuits for the Space Shuttle in the early 1970s, I performed my design calculations using slide rule and paper. By contrast, in a recent software project called OpticalRayTracer, I used one computer program to turn some first-principle optical equations into source code for another computer program (a Python library called "SymPy" efficiently converted a few key equations into many reliable lines of compilable Java code).

It may not be obvious in every profession, but the hidden meaning of many technological innovations is to make mathematics more obviously important, and easier as well. Over the decades it's come to me that my most creative work is, in one way or another, an expression of mathematical ideas. And in science, in part because of the computer revolution, it's becoming clear that a scientific theory without a mathematical expression isn't really science, it's philosophy.

This talk about mathematics may strike some readers as reductionism, as an oversimplified picture of modern times, but those at the forefront of the fastest-changing scientific and technological fields are becoming increasingly aware of the degree to which modern science and technology is driven by mathematical ideas.

Things have gotten to the point that, not only do we know what we know because of mathematics, but just as surely we know what we don't know, because of mathematics. As one important example, it's becoming clear that we've reached a time-horizon limit to our ability to forecast weather, for the simple reason that the sources of weather change arise in the quantum realm, a realm that lies beyond prediction except in a general statistical sense. This realization is well-established by the mathematics of quantum theory, our most successful physical theory.

Electric Duet is just one example of the role played by mathematics — I realized I might be able to make the Apple ][ speaker play decent music, if only I could write code that embodied the mathematical ideas behind signal processing.

When I was young I hated mathematics and thought it was useless drudgery. This was partly because of how badly mathematics is taught in U.S. public schools, but I wasn't very disciplined either. I learned most of my mathematics as an adult, unfortunately past the years when it would have come more easily, and every important job I've had required me to know more mathematics than I knew at that point in time. Even now, when I'm retired and choosing projects just because they'll be fun and entertaining, I need to know more mathematics (OpticalRayTracer is just one example).

To close this article I'll just say:

• Mathematics is much more important than most people realize,
• Mathematics shouldn't be confused with long division and adding columns of numbers, and
• As an adult you have the choice to learn mathematics, or be perpetually lied to by people who know more mathematics than you do.

Thanks for reading.

(Reader replies and comments.)

Mathematics | Detailed code listing?

Mathematics

First, I always enjoy your articles. Thank you. It seems I remember another article you wrote that had mentioned something about a coming (maybe it's here now) paradigm shift in teaching mathematics. I remember you using the analogy of no longer needing to memorize everything once printing became ubiquitous. Something along the lines of; with calculators and computers so readily available, now we need to know when to use the right type of math/math tool but not necessarily need to know how to execute every step. I did say that — it was in 1988 in an article (The Constancy of its Affections) I wrote for a magazine that doesn't exist any more. The article's views haven't been invalidated by the passage of time, in fact they've been largely confirmed — most of what I said there has come to pass. If I'm reading this article correctly it seems that maybe the ability to create Electric Duet came from a rigorous understanding of the math and even with modern tools that detail understanding was necessary. Yes, that's true. The only reason Electric Duet worked was because I was able to apply my knowledge of both mathematics and electronics to write a useful application, one that exploited a side effect of one of Steve Wozniak's early design choices. I'd really enjoy hearing more of your thoughts on the utilization of mathematical tools,their effect on teaching/learning math, and how that applies to future general population vs the future STEM population. People who know me may be able to anticipate how I would answer that inquiry. In today's society, in which a few people trained in mathematics have an implied obligation to educate or at least inform those who don't have that training, the difference between a linear and an exponential function will decide our future. Food production can at best increase linearly, but population naturally increases exponentially, and the result will be a catastrophe that's explained in my article "Peak People".

We could be taking steps to to avoid a population catastrophe, but there's no sign we're doing that, in fact many of our strictest policies are moving us in the opposite direction (by, for example, denying women basic civil rights and free access to birth control methods).

My point is that, in a perfect world, knowing mathematics would be an element in a well-rounded education, but in today's world it represents a safeguard against disaster. Author H. G. Wells said, "Civilization is in a race between education and catastrophe." With respect to the population issue, no truer words were ever spoken. Your articles always get me thinking. Thank you for that stimulation. You're welcome, and thanks for reading.

Detailed code listing?

Do you have a version of your Electric Duet Player with descriptive comments? I would love to see the listing with comments anyways, even if they do span several lines as you stated in your article. I thought I'd ask before I spent time attempting to write them myself. Over the years I've thought about this, but on reflection I realize the number of ways the routines' instructions interact, and given the many prior formulations that were eventually abandoned in favor of its present form, I decided an attempt to comment the source would make it even less comprehensible that it is at present.

Actually, a useful commentary on the code would need to list each path through the algorithm separately with a tally of machine cycles for that path, which means there wouldn't be just one listing, but about eight, for each possible path through the code.

As the main article explains, the key to the algorithm's success was to craft decision branches so that, regardless of which branch was executed, the number of loop machine cycles didn't change. I can remember spending hours thinking of ways to make that happen, regardless of which path the program took through the loop.

And then, after those issues were resolved through a series of interacting compromises, the loop time had to be some precise multiple of a recognizable musical frequency like 440 Hz, middle A. That additional requirement needed its own code tweaking after solving the other issues.

Guess how I tested the coding outcomes, in my kerosene-lantern-illuminated, wood-heated Oregon cabin? I used a tuning fork. No, really. Also, I didn't see any mention in your article of any attempts to simulate more than 2 voices at a time. If you did try it, were the results terrible? Electric Duet is truly mind blowing, though a 3 or 4 voice player would be even that much more mind blowing. Several issues. One, with each added voice, the ratio between the amplitude of the 8 KHz carrier frequency and the desired musical voices became less desirable, such that people who could still hear 8 KHz (i.e. people under about 40 years of age) would increasingly confuse the carrier's frequency with the music.

Two (actually expanding on point one), apart from the carrier-wave issue the amplitude of the separate musical voices declines with each added voice, since they're all being supported by the same carrier wave. Expressed simply, the maximum speaker amplitude shared between two voices gives each of them 1/2 the available amplitude, 1/3 for three and so forth. So a case of diminishing returns.

Also (tangentially) there's no way to change the amplitude of the individual voices with respect to each other, sort of like a harpsichord, which is one reason for my choice of example musical pieces — they couldn't rely too much on dynamics.

Three, because the Apple II clock frequency was fixed and the voices were being created by time multiplexing, two voices required a carrier frequency of 8 KHz, three voices would require 5 1/3 KHz, four would need 4 KHz. In other words, the carrier frequency would become more irritating with each added voice, especially for young people.

All this apart from the fact that Electric Duet's viability relied entirely on Apple not changing the clock frequency or adding anything that would interfere with a consistent motherboard clock rate. One example — to support use of a mouse, later Apple motherboards began to provide a hardware-triggered interrupt, and that interrupt destroyed my algorithm's timing.

For me personally, Electric Duet was a mathematical and engineering challenge more than an aesthetically pleasing music synthesizer, and young people in particular found the ever-present 8 KHz carrier frequency rather annoying. It was a series of compromises in a machine that was itself a series of compromises.

I hope this answers your inquiry. Thanks for writing!